
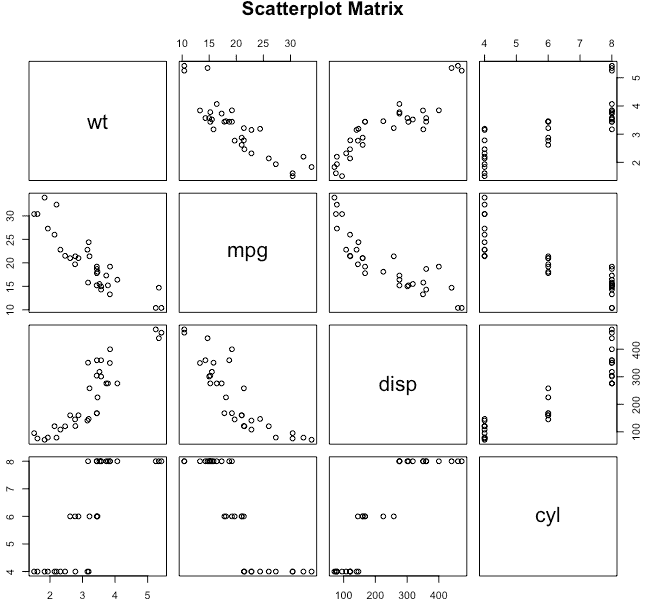
Under Matrix of plots, select the Simple plot. So, it is possible to write a macro to draw a " CompactMatrix" using the lattice layout, axis options and reference lines in GTL to create this graph. Creating a matrix of scatter plots between a set of variables is a good way to visualize the relationship between each pair of variables. But how do we do this now?įor SAS 9.2 and SAS 9.3, the ScatterPlotMatrix both in GTL and SGSCATTER already use the LAYOUT LATTICE in GTL to create this graph. Given that this arrangement is very popular, we will likely include an option to draw compact matrices in the next release based on the work shown here. Clinical concern levels are indicated by test case.Drawing of the upper triangle is eliminated resulting in a cleaner, uncluttered graph.The matrix occupies only a 3x3 grid for 4 variables hence uses the space more efficiently.All six pairwise combinations of the four variables are included in the graph.In fact, this arrangement is popular in the clinical domain as shown below in what can be called the "Compact Matrix". The upper triangle of the matrix is a mirror image of the lower triangle, and hence wasteful of the space.Ī closer examination of the graph indicates that we can eliminate the top row and right column of the matrix, to get a smaller 3x3 arrangement of the 4 variables, and still have all the pairwise scatterplot combinations for all the variables.To plot each circle with a different size, specify sz as a vector or a matrix. There is no way to indicate the clinical concern levels in the graphs. scatter(x,y,sz) specifies the circle sizes.To use the same size for all the circles, specify sz as a scalar.The matrix statement does not provide any way to customize the axes.There are a few issues with these graphs from a clinical perspective. Matrix asat alat alkph biltot / diagonal= (histogram normal ) Ods graphics / reset width=5in height=5.5in imagename= 'Matrix_4x4_Diag' You can assign different colors or markers to the levels of these variables.Title '4x4 Scatter Plot Matrix with Diagonals' A 2D array in which the rows are RGB or RGBA. Possible values: A scalar or sequence of n numbers to be mapped to colors using cmap and norm. You can use categorical or nominal variables to customize a scatter plot. carray-like or list of colors or color, optional The marker colors.
Either way, you are simply naming the different groups of data.
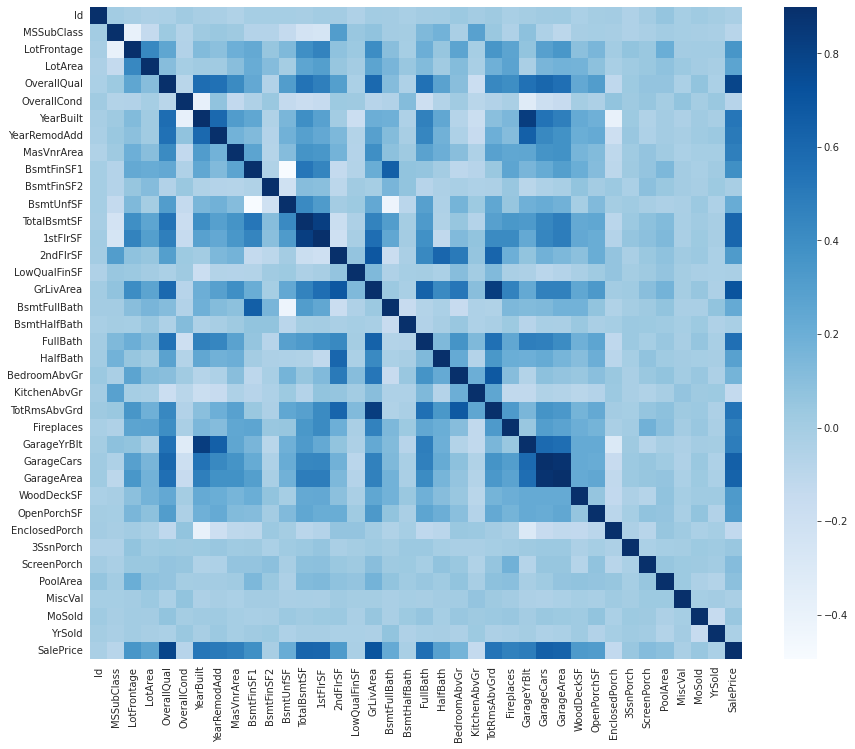
Scatterplot matrix code#
You can use the country abbreviation, or you can use numbers to code the country name. Country of residence is an example of a nominal variable. For example, in a survey where you are asked to give your opinion on a scale from “Strongly Disagree” to “Strongly Agree,” your responses are categorical.įor nominal data, the sample is also divided into groups but there is no particular order. With categorical data, the sample is divided into groups and the responses might have a defined order. Scatter plots are not a good option for categorical or nominal data, since these data are measured on a scale with specific values. Some examples of continuous data are:Ĭategorical or nominal data: use bar charts Scatter plots make sense for continuous data since these data are measured on a scale with many possible values. Scatter plots and types of data Continuous data: appropriate for scatter plots Annotations explaining the colors and markers could further enhance the matrix.įor your data, you can use a scatter plot matrix to explore many variables at the same time. The colors reveal that all these points are from cars made in the US, while the markers reveal that the cars are either sporty, medium, or large. There are several points outside the ellipse at the right side of the scatter plot.

From the density ellipse for the Displacement by Horsepower scatter plot, the reason for the possible outliers appear in the histogram for Displacement. In the Displacement by Horsepower plot, this point is highlighted in the middle of the density ellipse.īy deselecting the point, all points will appear with the same brightness, as shown in Figure 17. This point is also an outlier in some of the other scatter plots but not all of them. In Figure 16, the single blue circle that is an outlier in the Weight by Turning Circle scatter plot has been selected. It's possible to explore the points outside the circles to see if they are multivariate outliers. The red circles contain about 95% of the data. The scatter plot matrix in Figure 16 shows density ellipses in each individual scatter plot.


 0 kommentar(er)
0 kommentar(er)
